Helical Antenna
Introduction
This tutorial covers:
setup of a helix using the wire primitive
setup a lumped feeding port (R_in = 120 Ohms)
adding a near-field to far-field (nf2ff) box using an efficient subsampling
calculate the S-Parameter of the antenna
calculate and plot the far-field pattern
Python Script
Get the latest version from git.
Import Libraries
import os, tempfile
from pylab import *
from CSXCAD import CSXCAD
from openEMS import openEMS
from openEMS.physical_constants import *
Setup the simulation
Sim_Path = os.path.join(tempfile.gettempdir(), 'Helical_Ant')
post_proc_only = False
unit = 1e-3 # all length in mm
f0 = 2.4e9 # center frequency, frequency of interest!
lambda0 = round(C0/f0/unit) # wavelength in mm
fc = 0.5e9 # 20 dB corner frequency
Helix_radius = 20 # --> diameter is ~ lambda/pi
Helix_turns = 10 # --> expected gain is G ~ 4 * 10 = 40 (16dBi)
Helix_pitch = 30 # --> pitch is ~ lambda/4
Helix_mesh_res = 3
gnd_radius = lambda0/2
# feeding
feed_heigth = 3
feed_R = 120 #feed impedance
# size of the simulation box
SimBox = array([1, 1, 1.5])*2.0*lambda0
Setup FDTD parameter & excitation function
FDTD = openEMS(EndCriteria=1e-4)
FDTD.SetGaussExcite( f0, fc )
FDTD.SetBoundaryCond( ['MUR', 'MUR', 'MUR', 'MUR', 'MUR', 'PML_8'] )
Setup Geometry & Mesh
CSX = CSXCAD.ContinuousStructure()
FDTD.SetCSX(CSX)
mesh = CSX.GetGrid()
mesh.SetDeltaUnit(unit)
max_res = floor(C0 / (f0+fc) / unit / 20) # cell size: lambda/20
# create helix mesh
mesh.AddLine('x', [-Helix_radius, 0, Helix_radius])
mesh.SmoothMeshLines('x', Helix_mesh_res)
# add the air-box
mesh.AddLine('x', [-SimBox[0]/2-gnd_radius, SimBox[0]/2+gnd_radius])
# create a smooth mesh between specified fixed mesh lines
mesh.SmoothMeshLines('x', max_res, ratio=1.4)
# copy x-mesh to y-direction
mesh.SetLines('y', mesh.GetLines('x'))
# create helix mesh in z-direction
mesh.AddLine('z', [0, feed_heigth, Helix_turns*Helix_pitch+feed_heigth])
mesh.SmoothMeshLines('z', Helix_mesh_res)
# add the air-box
mesh.AddLine('z', [-SimBox[2]/2, max(mesh.GetLines('z'))+SimBox[2]/2 ])
# create a smooth mesh between specified fixed mesh lines
mesh.SmoothMeshLines('z', max_res, ratio=1.4)
Create the Geometry
Create the metal helix using the wire primitive.
Create a metal gorund plane as cylinder.
# create a perfect electric conductor (PEC)
helix_metal = CSX.AddMetal('helix' )
ang = linspace(0,2*pi,21)
coil_x = Helix_radius*cos(ang)
coil_y = Helix_radius*sin(ang)
coil_z = ang/2/pi*Helix_pitch
Helix_x=np.array([])
Helix_y=np.array([])
Helix_z=np.array([])
zpos = feed_heigth
for n in range(Helix_turns-1):
Helix_x = r_[Helix_x, coil_x]
Helix_y = r_[Helix_y, coil_y]
Helix_z = r_[Helix_z ,coil_z+zpos]
zpos = zpos + Helix_pitch
p = np.array([Helix_x, Helix_y, Helix_z])
helix_metal.AddCurve(p)
# create ground circular ground
gnd = CSX.AddMetal( 'gnd' ) # create a perfect electric conductor (PEC)
# add a box using cylindrical coordinates
start = [0, 0, -0.1]
stop = [0, 0, 0.1]
gnd.AddCylinder(start, stop, radius=gnd_radius)
# apply the excitation & resist as a current source
start = [Helix_radius, 0, 0]
stop = [Helix_radius, 0, feed_heigth]
port = FDTD.AddLumpedPort(1 ,feed_R, start, stop, 'z', 1.0, priority=5)
# nf2ff calc
nf2ff = FDTD.CreateNF2FFBox(opt_resolution=[lambda0/15]*3)
Run the simulation
if 0: # debugging only
CSX_file = os.path.join(Sim_Path, 'helix.xml')
if not os.path.exists(Sim_Path):
os.mkdir(Sim_Path)
CSX.Write2XML(CSX_file)
from CSXCAD import AppCSXCAD_BIN
os.system(AppCSXCAD_BIN + ' "{}"'.format(CSX_file))
if not post_proc_only:
FDTD.Run(Sim_Path, cleanup=True)
Postprocessing & plotting
freq = linspace( f0-fc, f0+fc, 501 )
port.CalcPort(Sim_Path, freq)
Zin = port.uf_tot / port.if_tot
s11 = port.uf_ref / port.uf_inc
Plot the feed point impedance
figure()
plot( freq/1e6, real(Zin), 'k-', linewidth=2, label=r'$\Re(Z_{in})$' )
grid()
plot( freq/1e6, imag(Zin), 'r--', linewidth=2, label=r'$\Im(Z_{in})$' )
title( 'feed point impedance' )
xlabel( 'frequency (MHz)' )
ylabel( 'impedance ($\Omega$)' )
legend( )
Plot reflection coefficient S11
figure()
plot( freq/1e6, 20*log10(abs(s11)), 'k-', linewidth=2 )
grid()
title( 'reflection coefficient $S_{11}$' )
xlabel( 'frequency (MHz)' )
ylabel( 'reflection coefficient $|S_{11}|$' )
Create the NFFF contour
calculate the far field at phi=0 degrees and at phi=90 degrees
theta = arange(0.,180.,1.)
phi = arange(-180,180,2)
disp( 'calculating the 3D far field...' )
nf2ff_res = nf2ff.CalcNF2FF(Sim_Path, f0, theta, phi, read_cached=True, verbose=True )
Dmax_dB = 10*log10(nf2ff_res.Dmax[0])
E_norm = 20.0*log10(nf2ff_res.E_norm[0]/np.max(nf2ff_res.E_norm[0])) + 10*log10(nf2ff_res.Dmax[0])
theta_HPBW = theta[ np.where(squeeze(E_norm[:,phi==0])<Dmax_dB-3)[0][0] ]
Display power and directivity
print('radiated power: Prad = {} W'.format(nf2ff_res.Prad[0]))
print('directivity: Dmax = {} dBi'.format(Dmax_dB))
print('efficiency: nu_rad = {} %'.format(100*nf2ff_res.Prad[0]/interp(f0, freq, port.P_acc)))
print('theta_HPBW = {} °'.format(theta_HPBW))
E_norm = 20.0*log10(nf2ff_res.E_norm[0]/np.max(nf2ff_res.E_norm[0])) + 10*log10(nf2ff_res.Dmax[0])
E_CPRH = 20.0*log10(np.abs(nf2ff_res.E_cprh[0])/np.max(nf2ff_res.E_norm[0])) + 10*log10(nf2ff_res.Dmax[0])
E_CPLH = 20.0*log10(np.abs(nf2ff_res.E_cplh[0])/np.max(nf2ff_res.E_norm[0])) + 10*log10(nf2ff_res.Dmax[0])
Plot the pattern
figure()
plot(theta, E_norm[:,phi==0],'k-' , linewidth=2, label='$|E|$')
plot(theta, E_CPRH[:,phi==0],'g--', linewidth=2, label='$|E_{CPRH}|$')
plot(theta, E_CPLH[:,phi==0],'r-.', linewidth=2, label='$|E_{CPLH}|$')
grid()
xlabel('theta (deg)')
ylabel('directivity (dBi)')
title('Frequency: {} GHz'.format(nf2ff_res.freq[0]/1e9))
legend()
show()
Images

3D view of the Helical Antenna (AppCSXCAD)
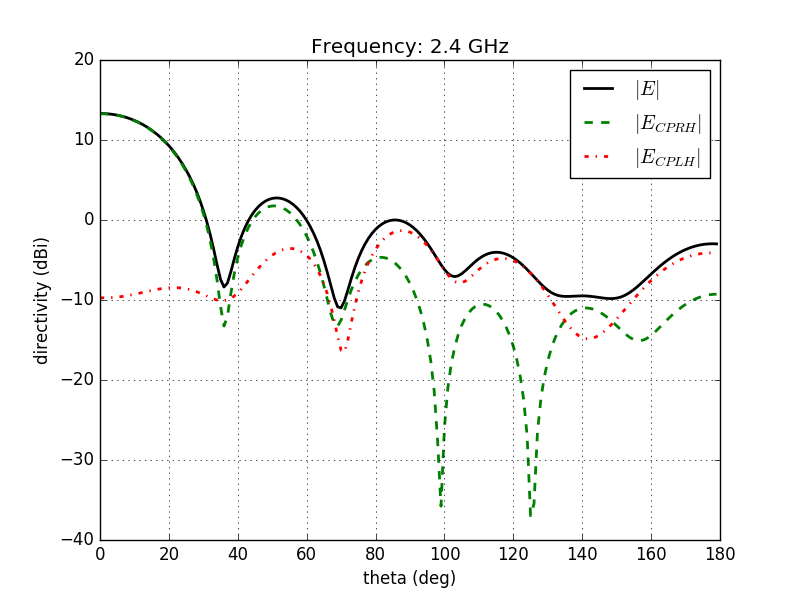
Far-Field pattern showing a right-handed circular polarization.